This page was built to translate between Miller and Miller-Bravais indices, to calculate the angle between given directions and the plane on which a lattice vector is normal to for both cubic and hexagonal crystal structures. For more information on crystallographic computations in the real and reciprocal space check this tutorial (pdf). We also recommend the following excellent textbook: “Structure of Materials: An Introduction to Crystallography, Diffraction and Symmetry” by M. De Graef and M. E. McHenry.
The 1st block, (hkl)⇔(hkil) converts Miller indices describing a set of planes to the equivalent Miller-Bravais indices through the following relationship:
\( i=-(h+k) \quad h=h \quad k=k \quad l=l. \)
1) Hexagonal Miller plane indices to Miller-Bravais indices and back:
(hkl)⇔(hkil)
( )
( )
For instance the crystallographic direction described in Miller indices as \( [uvw] \) is given by the translation vector \( \mathbf{t}= u\mathbf{a_1} + v\mathbf{a_2} + w\mathbf{c} \) in terms of the three basis vectors of the hexagonal lattice \( \{\mathbf{a_1}, \mathbf{a_2}, \mathbf{c}\} \). In terms of four vectors the same translation vector will be \( \mathbf{t} = U\mathbf{A_1} + V\mathbf{A_2} + T\mathbf{A_3} + W\mathbf{C} \) and will be described by the Miller-Bravais indices as \([UVTW]\) . The three vectors basis define the primitive hexagonal (hP) rhomboid prism cell (see drawing). The four vectors define a hexagonal prism cell made out of three hP cell. The following relations are true about the two basis sets: \( \mathbf{A_1}=\mathbf{a_1}, \quad \mathbf{A_2}=\mathbf{a_2}, \quad \mathbf{A_3}=-(\mathbf{a_1} + \mathbf{a_2}) , \quad \mathbf{C}=\mathbf{c} \).
The relations between the translation vector components in the two notation systems follows from the equality:
\(U\mathbf{A_1} + V\mathbf{A_2} + T\mathbf{A_3} + W\mathbf{C} = u\mathbf{a_1} + v\mathbf{a_2} + w\mathbf{c} \)
The 2nd block [uvw]⇔[UVTW] converts direction vectors written in Miller indices to Miller-Bravais indices and back through the following formulas:
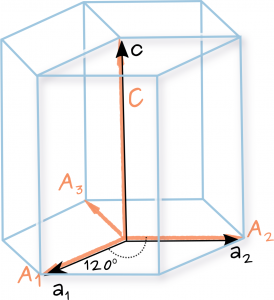
Hexagonal primitive cell made out of three hP unit cell together with the basis vectors describing them.
Miller \([uvw]\) ⇒ Miller-Bravais \( [UVTW]:\)
\( U=\frac{1}{3}(2u-v) \hspace{0.5cm}\)
\( V=\frac{1}{3}(2v-u)\hspace{0.5cm}\)
\( T=-(U+V) \hspace{0.5cm}\)
\( W=w \hspace{0.5cm}\)
Miller-Bravais \( [UVTW]\) ⇒ Miller \( [uvw]:\)
\( u = 2U+V \hspace{0.5cm}\)
\( v = 2V+U \hspace{0.5cm}\)
\( w=W\hspace{0.5cm}\)
As before, \(T\) is not independent and cannot be modified by the user.
2) Hexagonal Miller direction indices to Miller-Bravais indices and back:
[uvw]⇔[UVTW]
[ ]
[ ]
The dot product between two vectors \(\mathbf{p} = p_i \mathbf{a}_i\) and \(\mathbf{q} = q_i \mathbf{a}_i\) defined in a crystal system with lattice parameters \(\{a, b, c, \alpha, \beta, \gamma\}\) and basis vectors \(\{\mathbf{a_1}, \mathbf{a_2}, \mathbf{a_3}\}\) is given generally by:
\(\mathbf{p} \cdot \mathbf{q} = |\mathbf{p}| |\mathbf{q}| \cos{\theta} = p_i \mathbf{a}_i \cdot q_j \mathbf{a}_j = p_i g_{ij} q_j\)where \(g_{ij}\) is the direct matrix tensor defined as:
\( \begin{equation}g = \begin{bmatrix}
\mathbf{a_1} \cdot \mathbf{a_1} & \mathbf{a_1} \cdot \mathbf{a_2} & \mathbf{a_1} \cdot \mathbf{a_3} \\
\mathbf{a_2} \cdot \mathbf{a_1} & \mathbf{a_2} \cdot \mathbf{a_2} & \mathbf{a_2} \cdot \mathbf{a_3} \\
\mathbf{a_3} \cdot \mathbf{a_1} & \mathbf{a_3} \cdot \mathbf{a_2} & \mathbf{a_3} \cdot \mathbf{a_3}
\end{bmatrix} =
\begin{bmatrix}
a^2 & a b \cos{\gamma} & a c \cos{\beta} \\
b a \cos{\gamma} & b^2 & b c \cos{\alpha} \\
c a \cos{\beta} & c b \cos{\alpha} & c^2
\end{bmatrix}
\end{equation} \quad [1] \)
The angle \(\theta\) between the vectors \(\mathbf{p}\) and \(\mathbf{q}\) is then:
\( \theta = \cos^{-1}{\frac{p_i g_{ij} q_j}{\sqrt{p_i g_{ij} p_j} \sqrt{q_i g_{ij} q_j}}} \quad [2] \)
For a cubic crystal with lattice parameters \(\{a, a, a, 90, 90, 90\}\) the direct metric tensor reduces to:
\( g^{cub} =\begin{bmatrix}
a^2 & 0 & 0 \\
0 & a^2 & 0 \\
0 & 0 & a^2
\end{bmatrix} = a^2 \begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix} = a^2 \delta{ij}
\)
Which also means that the angle formula reduces to:
\( \theta = \cos^{-1}{\frac{p_i q_i}{\sqrt{p_i p_i} \sqrt{q_i q_i}}}\)
which is the formula we know from the Cartesian system.
The 3rd block, [u1 v1 w1] ∠ [u2 v2 w2], uses the dot product formula to calculate the cosine between two vectors \(\mathbf{V}_1=u_1\mathbf{a_1} +v_1\mathbf{a_2} + w_1\mathbf{a_3} \) and \(\mathbf{V_2}=u_2\mathbf{a_1} +v_2\mathbf{a_2} + w_2\mathbf{a_3} \) defined in a cubic crystal. The resulting angle is shown in both degrees and rads:
\( cos(\theta)=\displaystyle\frac{u_{1}u_{2}+v_{1}v_{2}+w_{1}w_{2}}{\sqrt{(u_1^2+v_1^2+w_1^2)(u_2^2+v_2^2+w_2^2)}}\)
3) Angle between two cubic directions:
[u1 v1 w1] ∠ [u2 v2 w2]
[ ] [ ]
= = =
\begin{bmatrix}
a^2 & -a^2/2 & 0 \\
-a^2/2 & a^2 & 0 \\
0 & 0 & c^2
\end{bmatrix}
\)
The magnitude of a vector, \(\mathbf{p}\), defined in a hexagonal crystal system, \(\mathbf{p}=p_1\mathbf{a_1}+p_2\mathbf{a_2}+p_3\mathbf{c}\) is then:
\( |\mathbf{p}| = \sqrt{p_i\,\, g^{hex}_{ij} \,\, p_j} = \sqrt{(a^2(p_1^2-p_1 p_2 +p_2^2) + c^2p_3^2)}\)
If we now consider two directions \([u_1 v_1 w_1]\) and \([u_2 v_2 w_2]\) defined this time in a hexagonal crystal with basis vectors \( \mathbf{a}_1, \mathbf{a}_2, \mathbf{c}\), then the angle between can be calculated from eq. [2] to be:
\( cos(\theta)=\displaystyle\frac{a^2\left(u_{1}u_{2} + v_{1}v_{2} -\frac{1}{2}(u_1 v_2+v_1 u_2)\right)+ c^2 w_{1}w_{2}}{\sqrt{a^2(u_1^2-u_1 v_1 + v_1^2) + c^2 w_1^2 } \sqrt{a^2(u_2^2 -u_2v_2+v_2^2) + c^2 w_2^2}}\)
The 4th block, [u1 v1 w1] ∠ [u2 v2 w2], calculates the angle between two hexagonal crystal direction given in Miller indices.
A similar equation can be derived for direction given in Miller-Bravais indices. The direct metric tensor for a hexagonal crystal system defined with the four-basis vectors is:
\( ^{hex}G=\begin{bmatrix}\mathbf{A_1} \cdot \mathbf{A_1} & \mathbf{A_1} \cdot \mathbf{A_2} & \mathbf{A_1} \cdot \mathbf{A_3} & \mathbf{A_1} \cdot \mathbf{C} \\
\mathbf{A_2} \cdot \mathbf{A_1} & \mathbf{A_2} \cdot \mathbf{A_2} & \mathbf{A_2} \cdot \mathbf{A_3} & \mathbf{A_2} \cdot \mathbf{C} \\
\mathbf{A_3} \cdot \mathbf{A_1} & \mathbf{A_3} \cdot \mathbf{A_2} & \mathbf{A_3} \cdot \mathbf{A_3} & \mathbf{A_3} \cdot \mathbf{C} \\
\mathbf{C} \cdot \mathbf{A_1} & \mathbf{C} \cdot \mathbf{A_2} & \mathbf{C} \cdot \mathbf{A_3} & \mathbf{C} \cdot \mathbf{C}
\end{bmatrix} =\frac{a^2}{2}\begin{bmatrix}
2 & -1 & -1 & 0 \\
-1 & 2 & -1 & 0 \\
-1 & -1 & 2 & 0 \\
0 & 0 & 0 & 2c^2/a^2
\end{bmatrix}.
\)
The magnitude of a vector, \(\mathbf{p}\), defined in a hexagonal crystal system this time using four bais vector: \(\mathbf{p}=P_1\mathbf{A_1}+P_2\mathbf{A_2}+P’\mathbf{A_3}+P_3\mathbf{C}\) is then:
\( |\mathbf{p}| = \sqrt{P_i\,\, ^{hex}{G}_{ij} \,\, P_j} = \sqrt{(3a^2(P_1^2+P_1 P_2 +P_2^2) + c^2P_3^2)}\)
The 5th block, [U1 V1 T1 W1] ∠ [U2 V2 T1 W2], uses the metric tensor \(G\) to the angle between two Miller-Bravais directions:
\( cos(\theta)=\displaystyle\frac{a^2\left( 3(U_{1}U_{2} + V_{1}V_{2}) + \frac{3}{2}(U_1 V_2+V_1 U_2)\right)+ c^2 W_{1}W_{2}}{\sqrt{3a^2(U_1^2+U_1 V_1 + V_1^2) + c^2 W_1^2 } \sqrt{3a^2(U_2^2 +U_2V_2+V_2^2) + c^2 W_2^2}}\)
.
4) Angle between two Miller hexagonal directions:
[u1 v1 w1] ∠ [u2 v2 w2]
Å Å
[ ] [ ]
= = =
5) Angle between two hexagonal Miller-Bravais directions:
[U1 V1 T1 W1] ∠ [U2 V2 T1 W2]
Å Å
[ ] [ ]
= = =
\)
6) Normal on a plane (hkl) in crystal coordinates for a cubic system:
[uvw] ⊥ (hkl)
( )
[ ]
For any other crystal structure, we need to solve the problem of transforming the reciprocal space vector \(\mathbf{g}_{hkl}\) coordinate from the reciprocal lattice \(\mathbf{a}^*_i\) to the real space lattice \(\mathbf{a}_i\). For this we need to use the definition of the reciprocal metric tensor \(g^*_{ij}\) this time: \(g_{ij}=\mathbf{a}^*_i \cdot \mathbf{a}^*_j\). For a vector \(\mathbf{p}=p_i \mathbf{a}^*_i\) with known components in the reciprocal space we can write its real space components:
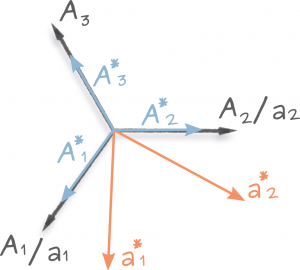
Real and reciprocal hexagonal lattice basis sets both in three and four vector notations.
\) For a hexagonal system the reciprocal metric tensor is: \( ^{hex}g^* = \begin{bmatrix}
\mathbf{a_1^*} \cdot \mathbf{a_1^*} & \mathbf{a_1^*} \cdot \mathbf{a_2^*} & \mathbf{a_1^*} \cdot \mathbf{c^*} \\
\mathbf{a_2^*} \cdot \mathbf{a_1^*} & \mathbf{a_2^*} \cdot \mathbf{a_2^*} & \mathbf{a_2^*} \cdot \mathbf{c^*} \\
\mathbf{c^*} \cdot \mathbf{a_1^*} & \mathbf{c^*} \cdot \mathbf{a_2^*} & \mathbf{c^*} \cdot \mathbf{c^*}
\end{bmatrix}=(^{hex}g)^{-1} =
\frac{2}{3a^2}\begin{bmatrix}
2 & 1 & 0 \\[6pt] 1 & 2 & 0 \\[6pt] 0 & 0 & \frac{3a^2}{2c^2}
\end{bmatrix}
\)
The components of \(\mathbf{g}_{hkl} = h \mathbf{a}^*_1 + k \mathbf{a}^*_2+ l \mathbf{c}^* = g_1 \mathbf{a}_1 + g_2 \mathbf{a}_2 +g_3 \mathbf{c}\) in the real space are then:
\( \begin{bmatrix} g_1 & g_2 & g_3 \end{bmatrix} = [h k l] \,\, ^{hex}g^* = \frac{2}{3a^2}\begin{bmatrix} 2h+ k & 2k +h & \frac{3a^2}{2c^2}l \end{bmatrix}\)
These fractions will not necessarily reduce to relative primitive integers and therefore we’re not guaranteed to find the Miller indices of this direction. This is the case since the reciprocal space and the real one do not align to each other.
The 7th block, [n1 n2 n3] ⊥ (hkl), calculates the relative primitive components, if they exist, of a vector \(\mathbf{n} = n_1 \mathbf{a}_1 + n_2 \mathbf{a}_2 + n_3 \mathbf{c}\) parallel to \(\mathbf{g}_{hkl}\):
\(
\begin{bmatrix} n_1 & n_2 & n_3 \end{bmatrix} = \begin{bmatrix} 2h+ k & 2k +h & \frac{3a^2}{2c^2}l \end{bmatrix}
\)
We can do the same thing in Miller-Bravais notation. The reciprocal metric tensor in four vector basis set notation is:
\( ^{hex}G^* =\frac{2}{9a^2}\begin{bmatrix}2 & -1 & -1 & 0 \\
-1 & 2 & -1 & 0 \\
-1 & -1 & 2 & 0 \\
0 & 0 & 0 & \frac{9a^2}{2c^2}
\end{bmatrix}
\)
The components of \(\mathbf{g}_{hkil} = h \mathbf{A}^*_1 + k \mathbf{A}^*_2 + i \mathbf{A}^*_3 + l \mathbf{C}^* = G_1 \mathbf{A}_1 + G_2 \mathbf{A}_2 + G’ \mathbf{A}_3 + G_3 \mathbf{C}\) in the real space are then:
\( \begin{bmatrix} G_1 & G_2 & G’ & G_3 \end{bmatrix} = [h k i l] \,\, ^{hex}G^* = \frac{2}{3a^2}\begin{bmatrix} h & k & -h-k & \frac{3a^2}{2c^2}l \end{bmatrix}\)
where we made use of the identity \(i=-(k+l)\).
The 8th block, [N1 N2 N’ N3] ⊥ (hkil), calculates the relative primitive components, if they exist, of a vector \(\mathbf{n} = N_1 \mathbf{A}_1 + N_2 \mathbf{A}_2 + N’ \mathbf{A}_3 + N_3 \mathbf{C}\) parallel to \(\mathbf{g}_{hkil}\):
\(
\begin{bmatrix} N_1 & N_2 & N’ & N_3 \end{bmatrix} = \begin{bmatrix} h & k & -h -k & \frac{3a^2}{2c^2}l \end{bmatrix}
\)
Note, that in both notation cases, as long as the plane under consideration contains the crystallographic \(\mathbf{c}\)-direction (\(l=0\)) then it is trivial to reduce the components of the normal vector to relative primes indices. Alternatively, if the plane has as normal the [001] direction then again the task is trivial. In any other case, the normal direction cannot be reduced to Miller/Miller-Bravais indices.
7) Normal on a plane (hkl) in crystal coordinates for a hexagonal system
in Miller indices:
[n1 n2 n3] ⊥ (hkl)
Å Å
( )
[ ]
8) Normal on a plane (hkil) in crystal coordinates for a hexagonal system
in Miller-Bravais indices:
[N1 N2 N’ N3] ⊥ (hkil)
Å Å
( )
[ ]
This tool was written in 2017 during an undergraduate summer project by Almpes Kotzai under the supervision of Dr Carol Trager-Cowan and Elena Pascal.
