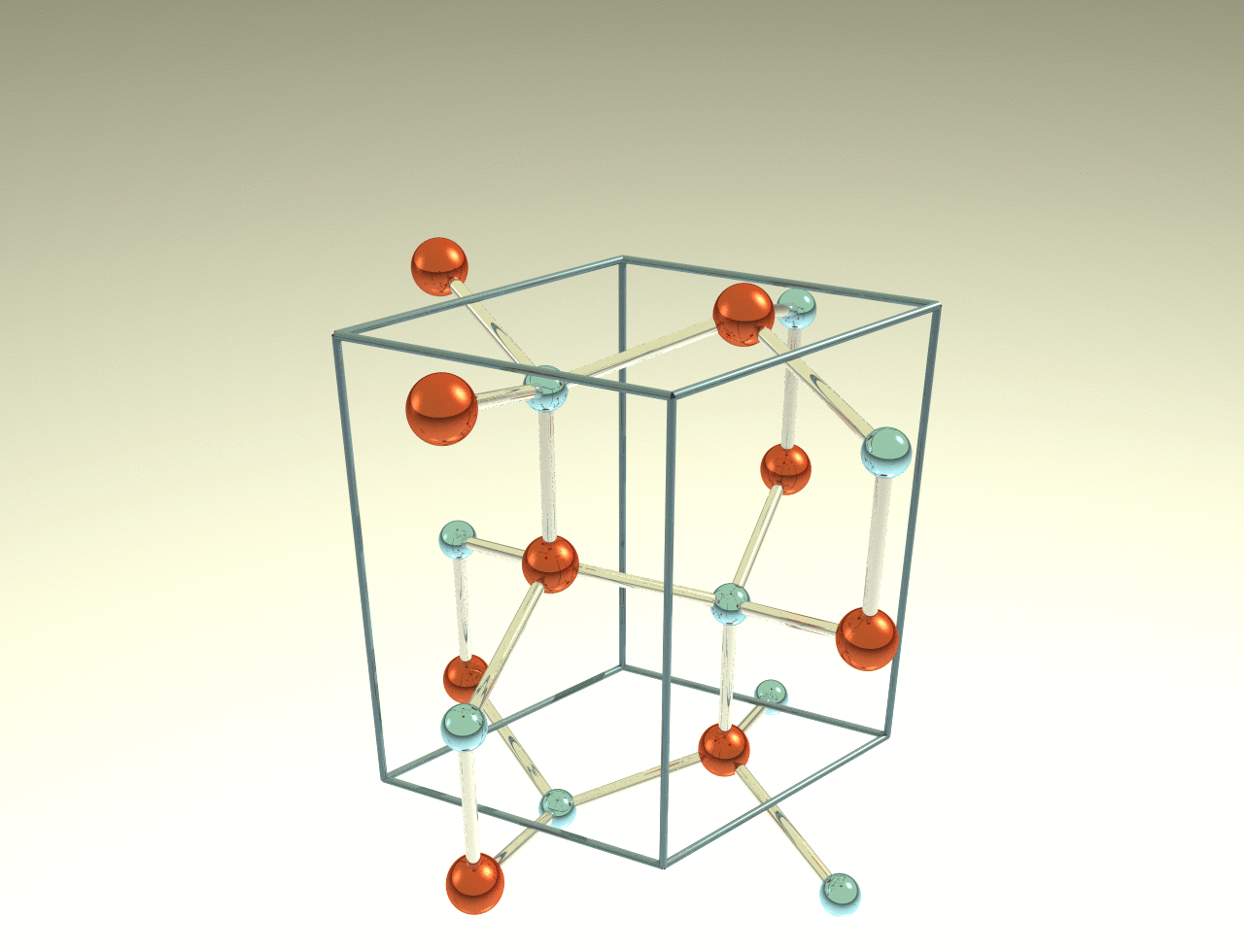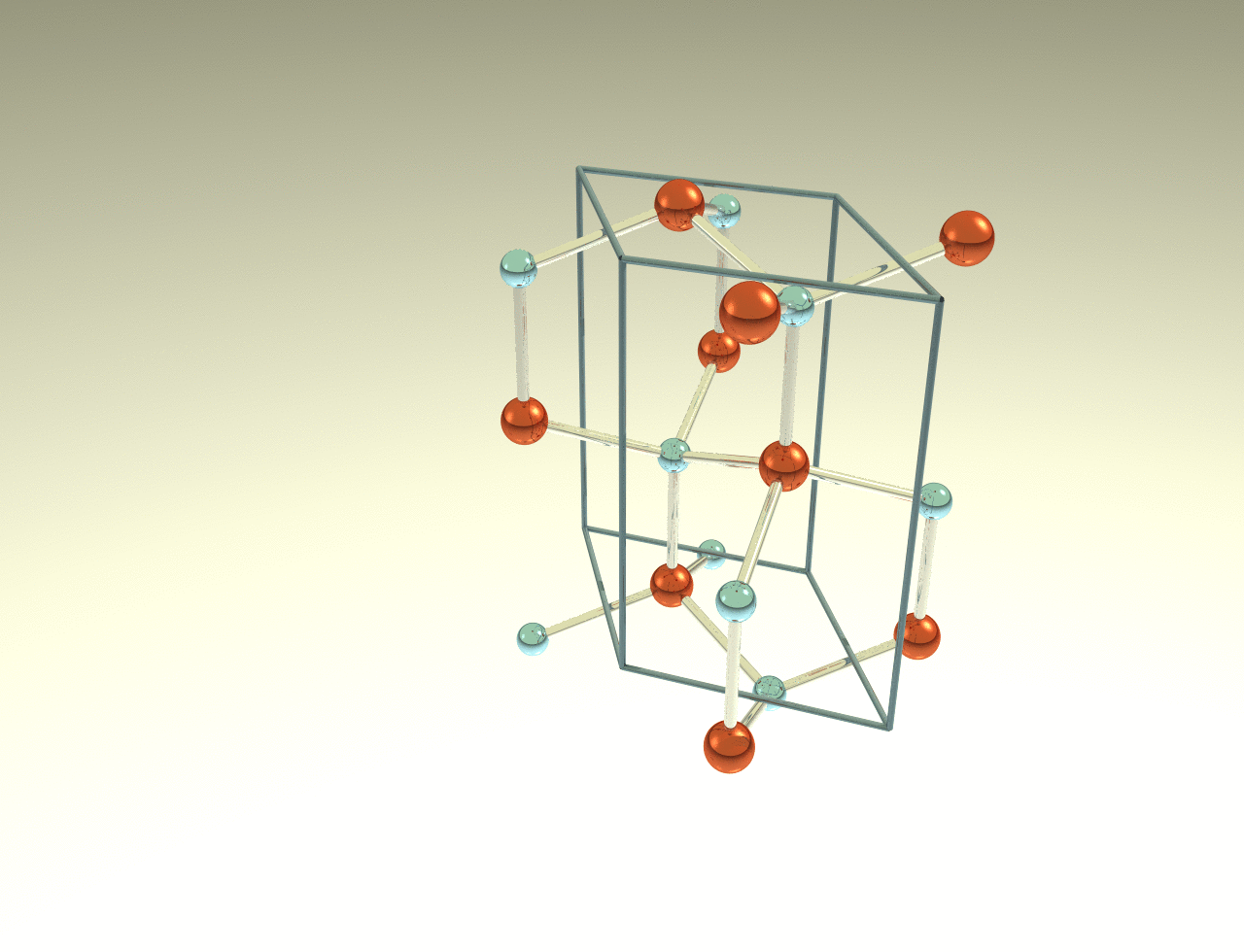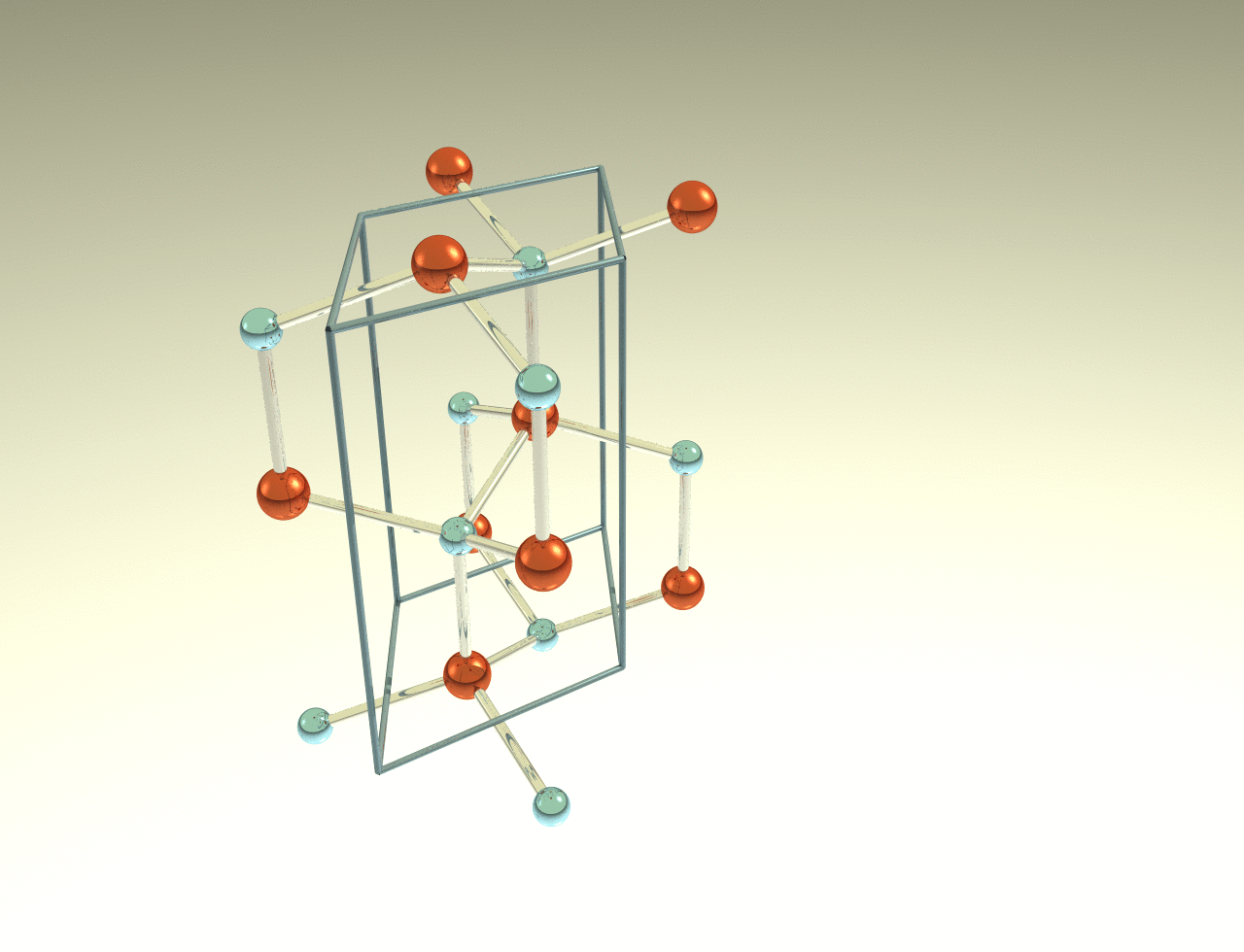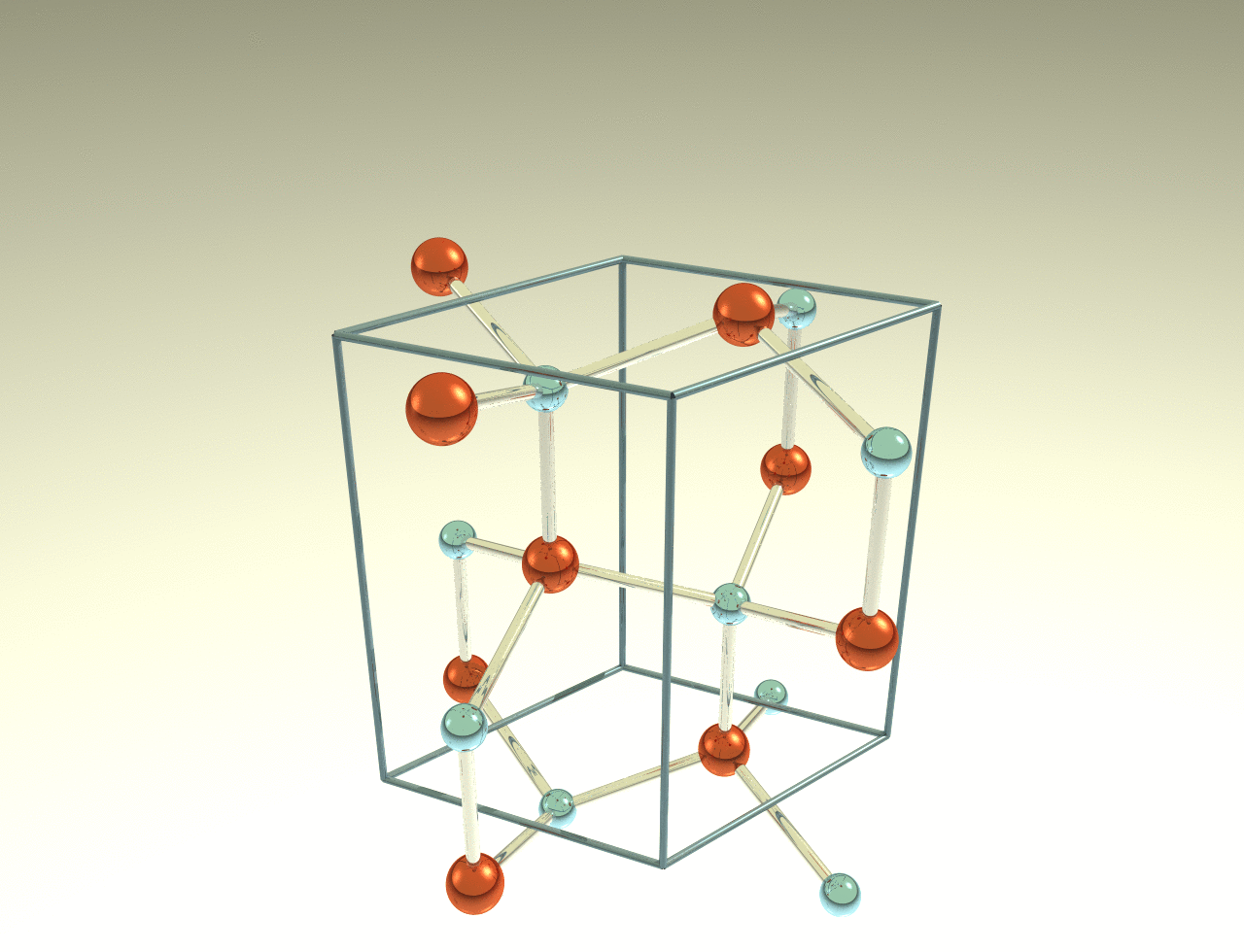
Wurtzite 2H
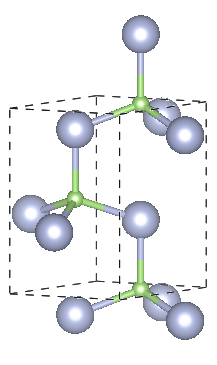
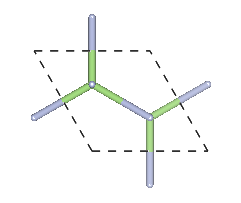
Crystal system: Hexagonal
Space Group: P63mc
Stacking Sequence: AB
A: 1⁄3 2⁄3 0
B: 1⁄3 2⁄3 3⁄8
Example: GaN
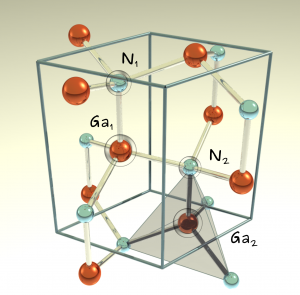
Wurtzite GaN unit cell containing four atoms. The tetrahedral dark box is the asymmetric unit cell.
Hexagonal 4H
![Depiction of Gallium Nitride in the form of 4H from the [001] direction](https://ssd.phys.strath.ac.uk/wp-content/uploads/GaN4H_w.png)
Crystal structure:1⁄2 Hexagonal – 1⁄2 Cubic
Space Group: P63mc
Stacking Sequence: ABCB
A1: 0 0 0
A2: 1⁄3 2⁄3 4⁄16
B1: 0 0 3⁄16
B2: 1⁄3 2⁄3 7⁄16
Example: ZnS
Note:
Clearly the fractions of the z component can be simplified further but that would not show the coherent symmetry of the model. One can see clearly in this form that the component ascends by four steps and alternates between even and odd numbers for the numerator but with equal denominator.
If one is even more precise in their observation, by correlating the 2H-4H-6H denominators, one can see how the pattern just repeats with the denominator being respectively half and three times less the size from 2H, something that makes sense since 4H, 6H are two and three times the size of 2H. This is truly a wonderful depiction of the spatial symmetry that these structures have.
The same applies for 3C, being a diamond structure and needing only 2 components and 9R which exhibits the same translational and spatial symmetry by alternating its x and y components and following the principles of the common denominator, representing a part of a whole.
Hexagonal 6H
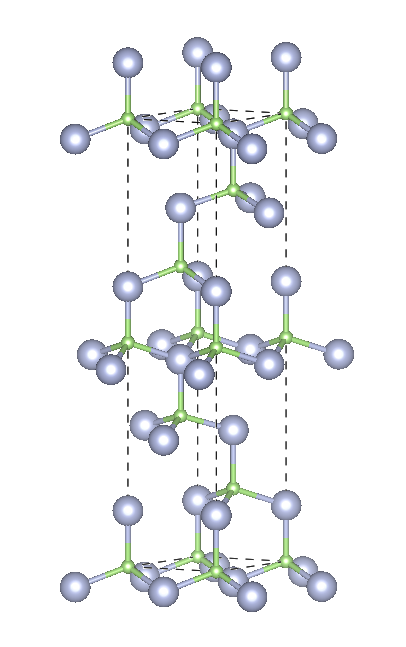
![Depiction of Gallium Nitride in the form of 6H from the [001] direction](https://ssd.phys.strath.ac.uk/wp-content/uploads/GaN6H_w.png)
Crystal structure: 2⁄3 Hexagonal – 1⁄3 Cubic
Space Group: P63mc
Stacking Sequence: ABCACB
A1: 0 0 0
A2: 1⁄3 2⁄3 4⁄24
A3: 2⁄3 1⁄3 8⁄24
B1: 0 0 3⁄24
B2: 1⁄3 2⁄3 7⁄24
B3: 2⁄3 1⁄3 11⁄24
Example: SiC
Note:
Clearly the fractions of the z component can be simplified further but that would not show the coherent symmetry of the model. One can see clearly in this form that the component ascends by four steps and alternates between even and odd numbers for the numerator but with equal denominator.
If one is even more precise in their observation, by correlating the 2H-4H-6H denominators, one can see how the pattern just repeats with the denominator being respectively half and three times less the size from 2H, something that makes sense since 4H, 6H are two and three times the size of 2H. This is truly a wonderful depiction of the spatial symmetry that these structures have.
The same applies for 3C, being a diamond structure and needing only 2 components and 9R which exhibits the same translational and spatial symmetry by alternating its x and y components and following the principles of the common denominator, representing a part of a whole.
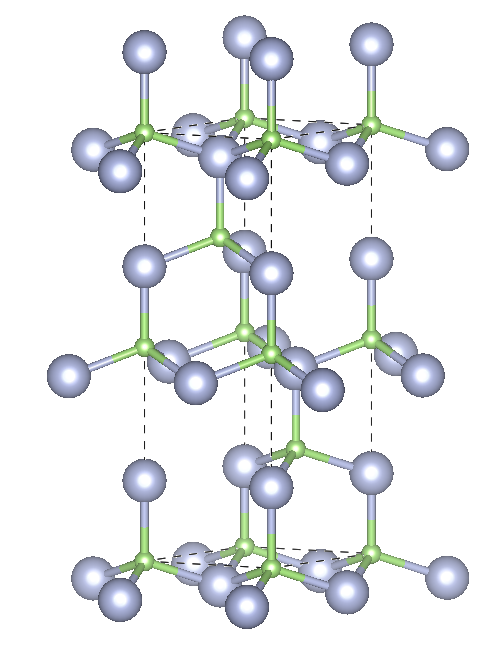
Zincblende 3C
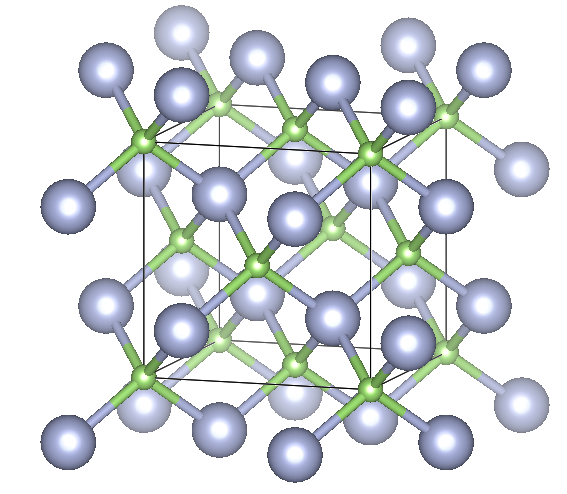
![Depiction of Gallium Nitride in the form of 3C in the [100] direction](https://ssd.phys.strath.ac.uk/wp-content/uploads/GaN3C_center.png)
Crystal system: Cubic
Space group: F43m
Stacking Sequence: ABC
A: 0 0 0
B: 1⁄4 1⁄4 1⁄4
Example: GaN
Rhombohedral 9R
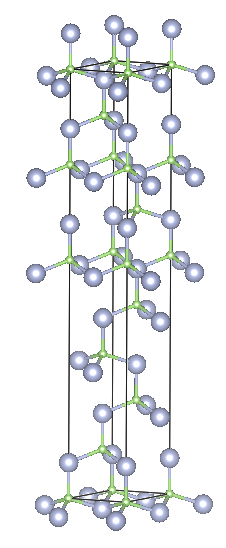
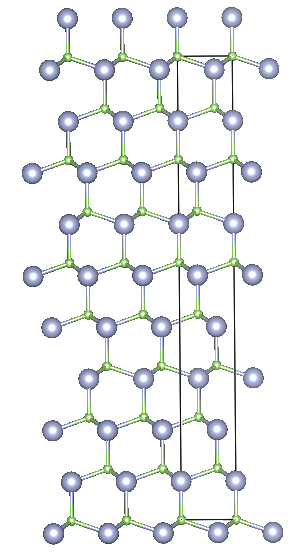
Crystal structure: 2⁄3 Cubic – 1⁄3 Hexagonal
Space Group: R3m(Hexagonal axes)
Stacking Sequence: CBABACACB
A1: 0 0 0
A2: 2⁄3 1⁄3 4⁄36
A3: 1⁄3 2⁄3 8⁄36
B1: 0 0 3⁄60
B2: 2⁄3 1⁄3 7⁄36
B3: 1⁄3 2⁄3 11⁄36
![Depiction of Gallium Nitride in the form of 9R from the [001] direction](https://ssd.phys.strath.ac.uk/wp-content/uploads/9R_top.png)
Example: SiC
Note:
Clearly the fractions of the z component can be simplified further but that would not show the coherent symmetry of the model. One can see clearly in this form that the component ascends by four steps and alternates between even and odd numbers for the numerator but with equal denominator.
If one is even more precise in their observation, by correlating the 2H-4H-6H denominators, one can see how the pattern just repeats with the denominator being respectively half and three times less the size from 2H, something that makes sense since 4H, 6H are two and three times the size of 2H. This is truly a wonderful depiction of the spatial symmetry that these structures have.
The same applies for 3C, being a diamond structure and needing only 2 components and 9R which exhibits the same translational and spatial symmetry by alternating its x and y components and following the principles of the common denominator, representing a part of a whole.
Blue and green images were produced using VESTA [1] by Almpes Kotzai under the supervision of Dr Carol Trager-Cowan. Yellow, orange and blue images made by Elena Pascal using Rayshade 4.0.9 software based on imput files developed by Marc De Graef [2].
[Bibtex]
@Article{Momma:db5098,
author = {Momma, Koichi and Izumi, Fujio},
title = {VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data},
journal = {Journal of Applied Crystallography},
year = {2011},
volume = {44},
number = {6},
pages = {1272--1276},
month = {Dec},
abstract = {VESTA is a three-dimensional visualization system for crystallographic studies and electronic state calculations. It has been upgraded to the latest version, VESTA3, implementing new features including drawing the external morphology of crystals; superimposing multiple structural models, volumetric data and crystal faces; calculation of electron and nuclear densities from structure parameters; calculation of Patterson functions from structure parameters or volumetric data; integration of electron and nuclear densities by Voronoi tessellation; visualization of isosurfaces with multiple levels; determination of the best plane for selected atoms; an extended bond-search algorithm to enable more sophisticated searches in complex molecules and cage-like structures; undo and redo in graphical user interface operations; and significant performance improvements in rendering isosurfaces and calculating slices.},
doi = {10.1107/S0021889811038970}
}[Bibtex]
@Misc{teachingPointGroup,
author = {De Graef, M.},
title = {Teaching crystallographic and magnetic point group symmetry using three-dimensional rendered visualizations},
howpublished = {International Union of Crystallography},
year = {2008},
url = {https://www.iucr.org/education/pamphlets/23/full-text},
}